Approximation of functions in Lipschitz class with Muckenhoupt Weights Lip (α,p,w) Using Matrix Operator

Abstract

Let f be a function where f∈L^p [0,2π] and p≥1 , and assume it to be a periodic function with (2π) period, and let the partial arithmetic sequence for Fourier Series s_n for this function to be given as follow:

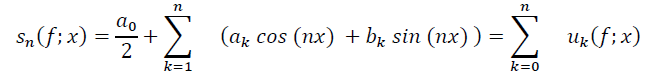
In this research, we will get to know about the functions in the class Lip (α,p,w) and then we will approximate these functions to a degree
O((n+1)^(-α) ), by using a by using t_n^A matrix operator and apply it on general term for partial arithmetic sequence Fourier series